Research
My research has focused on methods for discovering and modeling complex physical systems from data. I use approaches from machine learning (especially neural networks and sparse regression) for dynamical systems model discovery and systems identification. I am particularly interested in how machine learning can be leveraged to discover interpretable models.
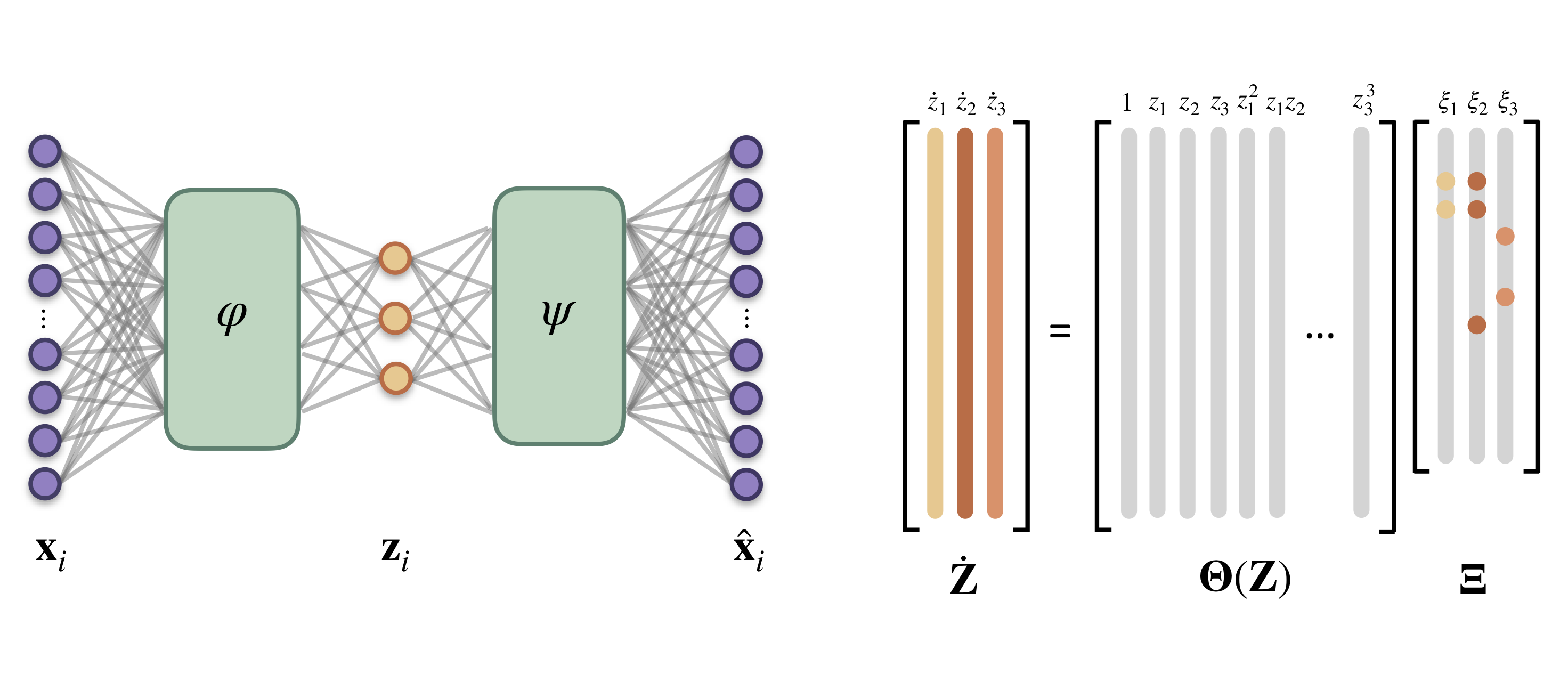
Simultaneous discovery of coordinates and governing equations. My recent work focuses on the discovery of parsimonious nonlinear governing equations from high-dimensional dynamical data. We developed a flexible autoencoder framework that simultaneously identifies a set of reduced coordinates and associated dynamical model. This work is available in PNAS. Associated code can be found on github.
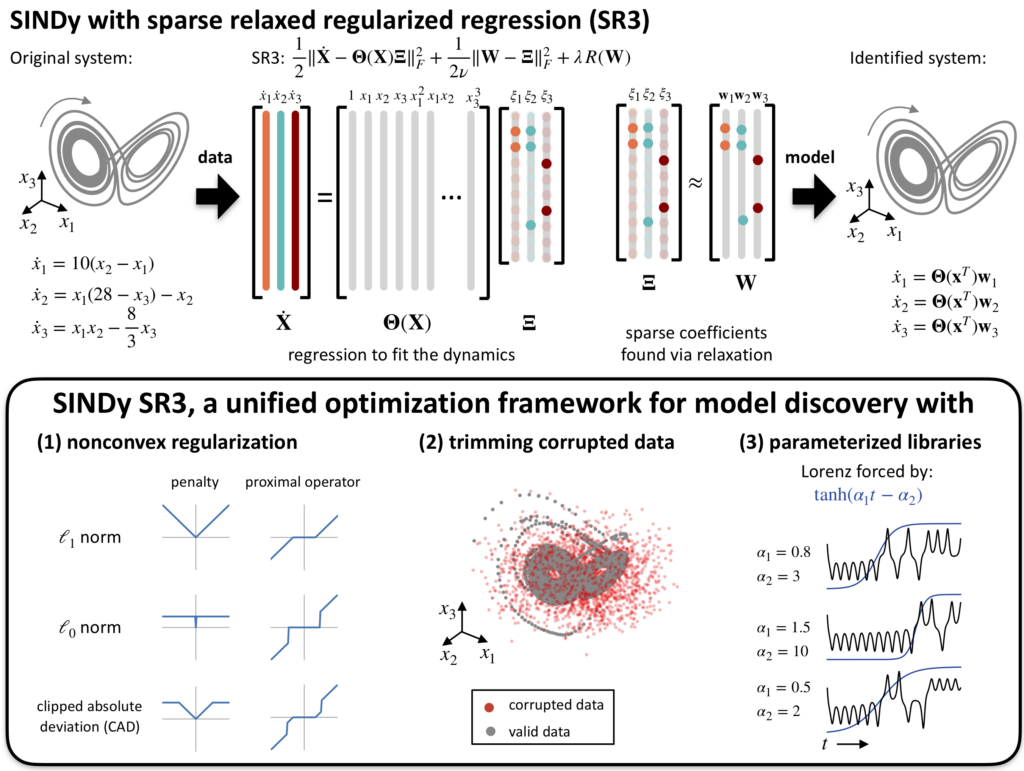
A unified sparse optimization framework to learn parsimonious physics-informed models from data. Applying machine learning approaches to scientific data often requires custom adaptations to handle application-specific challenges, such as physical constraints, data outliers, and parametric dependencies. We present a unified framework for learning nonlinear dynamical systems from data by combining SINDy with the recent SR3 optimization approach. We demonstrate how this approach can be used to handle nonconvex regularization, trimming of outliers, and parametric dependencies This work is available as an arXiv preprint.
PySINDy: an open-source Python package for identifying nonlinear dynamical systems from data. Together with fellow Ph.D. student Brian de Silva, I am developing a software package for applying SINDy to data. The package is designed to work well for both inexperienced practitioners who want to try out basic SINDy functionality and advanced users looking to customize the approach. It follows object-oriented design, is scikit-learn compatible, and implements a number of advanced options such as customizable function libraries, optimization algorithms, and differentiation methods.
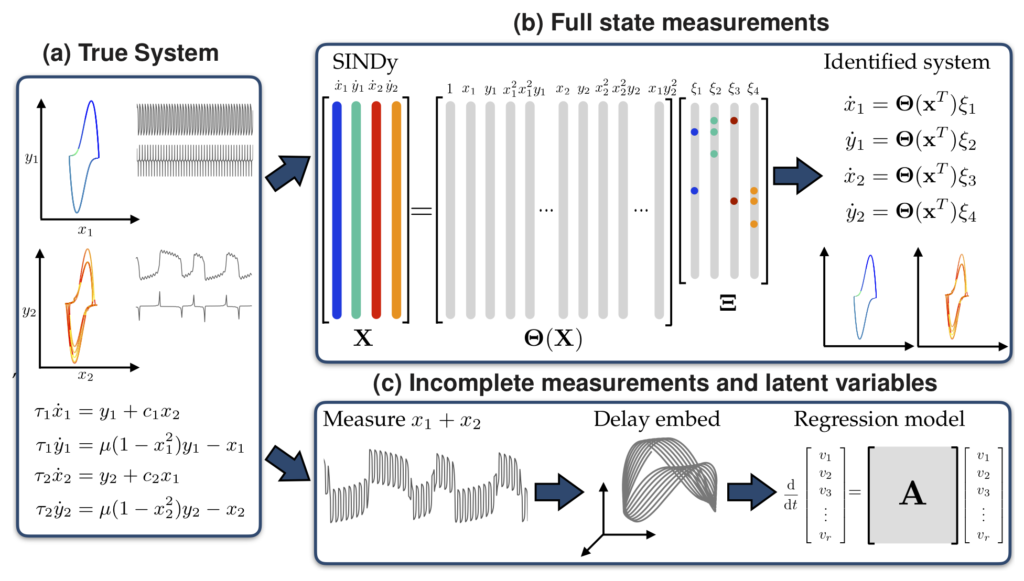
Sampling strategies for data-driven discovery of multiscale systems. Systems with multiscale dynamics present numerous challenges for data-driven methods. We developed a set of sampling strategies that reduce the data requirement for modeling and discovering multiscale dynamical systems from data, focusing in particular on sparse identification of nonlinear dynamics (SINDy) and Hankel alternative view of Koopman (HAVOK). This work can be found here with associated code available on github.
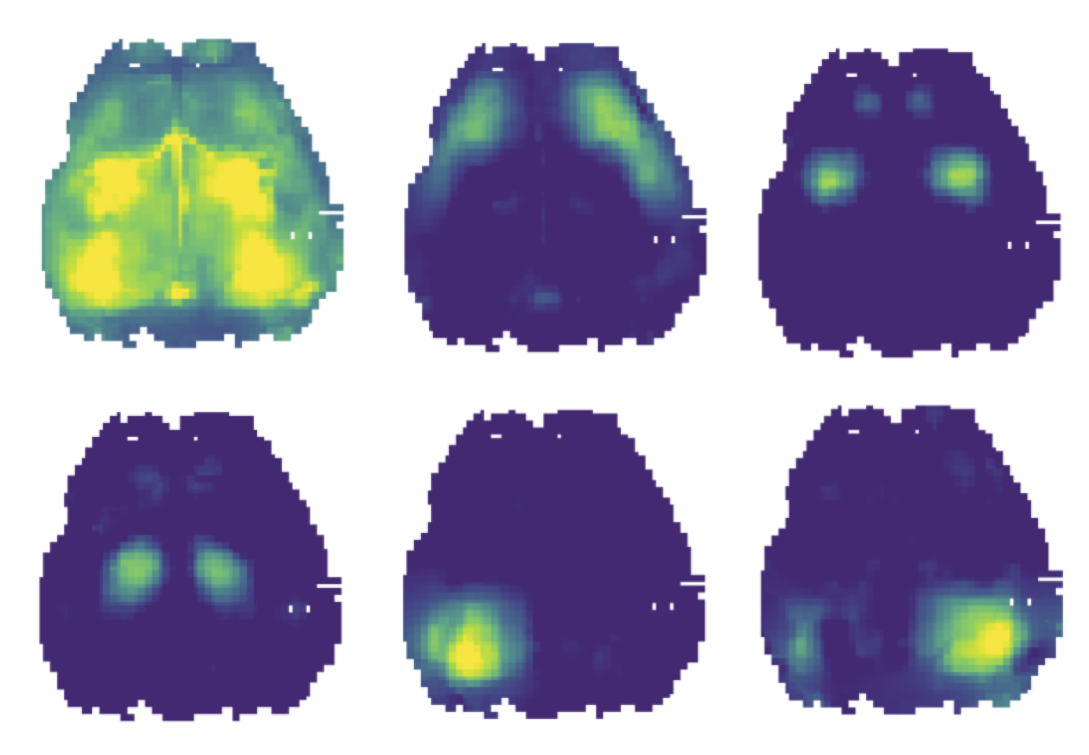
Dynamical modeling of brain-wide activity. Working with Eric Shea-Brown, I have collaborated with scientists at the Allen Institute for Brain Science on modeling the dynamics of whole-cortex activity during learning. We use latent variable models and regression frameworks to model and study the dynamics of widefield calcium imaging data from mice throughout the learning of a task. This work is currently in preparation for publication.
